How to Read Standard Deviaiton in Ercent Change

In statistics, a measure of variation

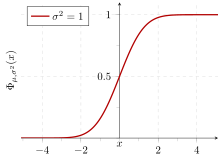
Cumulative probability of a normal distribution with expected value 0 and standard deviation ane

In statistics, the standard difference is a measure of the amount of variation or dispersion of a prepare of values.^[1] A low standard deviation indicates that the values tend to exist close to the hateful (also chosen the expected value) of the gear up, while a loftier standard departure indicates that the values are spread out over a wider range.

Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations past the lower case Greek letter of the alphabet sigma σ, for the population standard deviation, or the Latin letter due south, for the sample standard difference.

The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in do less robust, than the average absolute deviation.^{[2] [three]} A useful property of the standard deviation is that, unlike the variance, it is expressed in the same unit every bit the data.

The standard deviation of a population or sample and the standard error of a statistic (e.yard., of the sample mean) are quite different, merely related. The sample hateful's standard error is the standard difference of the set of ways that would exist found by drawing an infinite number of repeated samples from the population and computing a mean for each sample. The mean'due south standard error turns out to equal the population standard divergence divided past the square root of the sample size, and is estimated by using the sample standard deviation divided past the square root of the sample size. For case, a poll's standard mistake (what is reported as the margin of error of the poll), is the expected standard departure of the estimated mean if the same poll were to be conducted multiple times. Thus, the standard error estimates the standard deviation of an estimate, which itself measures how much the estimate depends on the particular sample that was taken from the population.

In science, it is common to report both the standard departure of the data (as a summary statistic) and the standard mistake of the guess (as a measure out of potential fault in the findings). By convention, merely effects more than two standard errors away from a zip expectation are considered "statistically significant", a safeguard against spurious conclusion that is really due to random sampling fault.

When only a sample of data from a population is available, the term standard deviation of the sample or sample standard deviation tin can refer to either the above-mentioned quantity as applied to those data, or to a modified quantity that is an unbiased estimate of the population standard deviation (the standard divergence of the entire population).

Basic examples [edit]

Population standard deviation of grades of eight students [edit]

Suppose that the entire population of interest is eight students in a item course. For a finite set of numbers, the population standard divergence is found by taking the foursquare root of the average of the squared deviations of the values subtracted from their average value. The marks of a form of eight students (that is, a statistical population) are the following eight values:

${\displaystyle two,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9.}$

These eight data points have the mean (average) of 5:

${\displaystyle \mu ={\frac {ii+4+four+iv+v+five+7+9}{8}}={\frac {40}{8}}=5.}$

First, calculate the deviations of each data point from the mean, and square the effect of each:

${\displaystyle {\brainstorm{assortment}{lll}(two-v)^{2}=(-iii)^{2}=9&&(5-v)^{two}=0^{ii}=0\\(4-v)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{two}=0\\(four-5)^{ii}=(-one)^{2}=one&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{ii}=4^{2}=16.\\\end{array}}}$

The variance is the mean of these values:

${\displaystyle \sigma ^{2}={\frac {9+i+1+1+0+0+iv+16}{8}}={\frac {32}{8}}=4.}$

and the population standard difference is equal to the square root of the variance:

${\displaystyle \sigma ={\sqrt {4}}=2.}$

This formula is valid but if the viii values with which we began form the complete population. If the values instead were a random sample drawn from some large parent population (for case, they were 8 students randomly and independently chosen from a class of ii million), then one divides past 7 (which is n − 1) instead of viii (which is northward) in the denominator of the last formula, and the result is ${\textstyle s={\sqrt {32/seven}}\approx ii.1.}$ In that case, the result of the original formula would be called the sample standard deviation and denoted by s instead of ${\displaystyle \sigma .}$ Dividing by n − i rather than by n gives an unbiased guess of the variance of the larger parent population. This is known as Bessel'south correction.^{[4] [5]} Roughly, the reason for it is that the formula for the sample variance relies on computing differences of observations from the sample mean, and the sample mean itself was constructed to exist as close as possible to the observations, and then just dividing by n would underestimate the variability.

Standard difference of average height for adult men [edit]

If the population of interest is approximately normally distributed, the standard departure provides information on the proportion of observations above or beneath certain values. For case, the average height for developed men in the Us is about 70 inches (177.8 cm), with a standard departure of effectually 3 inches (seven.62 cm). This means that nigh men (about 68%, assuming a normal distribution) take a height inside iii inches (7.62 cm) of the mean (67–73 inches (170.eighteen–185.42 cm)) – one standard departure – and almost all men (near 95%) accept a height inside 6 inches (fifteen.24 cm) of the mean (64–76 inches (162.56–193.04 cm)) – two standard deviations. If the standard divergence were nothing, then all men would exist exactly 70 inches (177.8 cm) tall. If the standard deviation were twenty inches (50.viii cm), then men would have much more variable heights, with a typical range of nearly 50–xc inches (127–228.six cm). 3 standard deviations account for 99.seven% of the sample population existence studied, bold the distribution is normal or bell-shaped (come across the 68–95–99.7 rule, or the empirical rule, for more information).

Definition of population values [edit]

Let μ be the expected value (the average) of random variable Ten with density f(x):

$${\displaystyle \mu \equiv \operatorname {Eastward} [X]=\int _{-\infty }^{+\infty }xf(ten)\,dx}$$

The standard deviation σ of Ten is divers as

$${\displaystyle \sigma \equiv {\sqrt {\operatorname {E} \left[(X-\mu )^{2}\right]}}={\sqrt {\int _{-\infty }^{+\infty }(x-\mu )^{2}f(ten)\,dx}},}$$

which tin exist shown to equal ${\textstyle {\sqrt {\operatorname {E} \left[Ten^{2}\right]-(\operatorname {Due east} [10])^{ii}}}.}$

Using words, the standard departure is the square root of the variance of X.

The standard deviation of a probability distribution is the aforementioned every bit that of a random variable having that distribution.

Not all random variables have a standard departure. If the distribution has fat tails going out to infinity, the standard divergence might not exist, because the integral might not converge. The normal distribution has tails going out to infinity, but its mean and standard deviation practise exist, considering the tails diminish rapidly enough. The Pareto distribution with parameter ${\displaystyle \alpha \in (one,2]}$ has a mean, but not a standard deviation (loosely speaking, the standard divergence is space). The Cauchy distribution has neither a mean nor a standard deviation.

Discrete random variable [edit]

In the example where Ten takes random values from a finite data set 10 ₁, x ₂, …, x_Northward , with each value having the same probability, the standard deviation is

$${\displaystyle \sigma ={\sqrt {{\frac {one}{Northward}}\left[(x_{1}-\mu )^{two}+(x_{2}-\mu )^{2}+\cdots +(x_{Northward}-\mu )^{2}\right]}},{\text{ where }}\mu ={\frac {1}{N}}(x_{1}+\cdots +x_{N}),}$$

or, by using summation notation,

$${\displaystyle \sigma ={\sqrt {{\frac {1}{Due north}}\sum _{i=i}^{N}(x_{i}-\mu )^{2}}},{\text{ where }}\mu ={\frac {ane}{Due north}}\sum _{i=ane}^{N}x_{i}.}$$

If, instead of having equal probabilities, the values accept different probabilities, let x _i have probability p _i, x _two have probability p ₂, …, x _N have probability p _N . In this case, the standard deviation volition be

$${\displaystyle \sigma ={\sqrt {\sum _{i=1}^{N}p_{i}(x_{i}-\mu )^{2}}},{\text{ where }}\mu =\sum _{i=1}^{N}p_{i}x_{i}.}$$

Continuous random variable [edit]

The standard deviation of a continuous real-valued random variable X with probability density function p(10) is

$${\displaystyle \sigma ={\sqrt {\int _{\mathbf {X} }(ten-\mu )^{2}\,p(x)\,dx}},{\text{ where }}\mu =\int _{\mathbf {10} }ten\,p(x)\,dx,}$$

and where the integrals are definite integrals taken for x ranging over the prepare of possible values of the random variable10.

In the example of a parametric family of distributions, the standard difference can exist expressed in terms of the parameters. For example, in the case of the log-normal distribution with parameters μ and σ ², the standard departure is

$${\displaystyle {\sqrt {\left(e^{\sigma ^{ii}}-1\right)eastward^{2\mu +\sigma ^{two}}}}.}$$

Estimation [edit]

I tin can find the standard deviation of an unabridged population in cases (such as standardized testing) where every member of a population is sampled. In cases where that cannot exist washed, the standard difference σ is estimated by examining a random sample taken from the population and computing a statistic of the sample, which is used equally an estimate of the population standard difference. Such a statistic is called an computer, and the estimator (or the value of the estimator, namely the estimate) is chosen a sample standard deviation, and is denoted by s (possibly with modifiers).

Unlike in the case of estimating the population mean, for which the sample mean is a simple estimator with many desirable properties (unbiased, efficient, maximum likelihood), in that location is no single calculator for the standard deviation with all these properties, and unbiased estimation of standard deviation is a very technically involved problem. Well-nigh ofttimes, the standard departure is estimated using the corrected sample standard deviation (using N − 1), defined below, and this is ofttimes referred to as the "sample standard deviation", without qualifiers. However, other estimators are better in other respects: the uncorrected estimator (using N) yields lower hateful squared error, while using N − 1.5 (for the normal distribution) about completely eliminates bias.

Uncorrected sample standard deviation [edit]

The formula for the population standard deviation (of a finite population) can be applied to the sample, using the size of the sample as the size of the population (though the bodily population size from which the sample is fatigued may be much larger). This estimator, denoted past s _N , is known equally the uncorrected sample standard deviation, or sometimes the standard deviation of the sample (considered every bit the entire population), and is defined as follows:^[six]

$${\displaystyle s_{N}={\sqrt {{\frac {1}{Due north}}\sum _{i=one}^{N}\left(x_{i}-{\bar {10}}\correct)^{2}}},}$$

where ${\displaystyle \{x_{1},\,x_{2},\,\ldots ,\,x_{N}\}}$ are the observed values of the sample items, and ${\displaystyle {\bar {x}}}$ is the hateful value of these observations, while the denominatorN stands for the size of the sample: this is the square root of the sample variance, which is the average of the squared deviations well-nigh the sample mean.

This is a consistent estimator (it converges in probability to the population value as the number of samples goes to infinity), and is the maximum-likelihood estimate when the population is unremarkably distributed.^{[ citation needed ]} However, this is a biased reckoner, as the estimates are generally too low. The bias decreases as sample size grows, dropping off as 1/Northward, and thus is most significant for small or moderate sample sizes; for ${\displaystyle North>75}$ the bias is below 1%. Thus for very large sample sizes, the uncorrected sample standard departure is generally adequate. This computer also has a uniformly smaller mean squared error than the corrected sample standard deviation.

Corrected sample standard deviation [edit]

If the biased sample variance (the second key moment of the sample, which is a downwardly-biased judge of the population variance) is used to compute an gauge of the population's standard difference, the result is

${\displaystyle s_{Due north}={\sqrt {{\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}-{\bar {ten}}\right)^{2}}}.}$

Here taking the square root introduces further downwardly bias, by Jensen'southward inequality, due to the square root's existence a concave role. The bias in the variance is easily corrected, but the bias from the foursquare root is more difficult to correct, and depends on the distribution in question.

An unbiased estimator for the variance is given past applying Bessel'southward correction, using N − 1 instead of Due north to yield the unbiased sample variance, denoted due south ^two:

${\displaystyle southward^{2}={\frac {1}{N-1}}\sum _{i=one}^{North}\left(x_{i}-{\bar {x}}\right)^{two}.}$

This estimator is unbiased if the variance exists and the sample values are drawn independently with replacement. N − 1 corresponds to the number of degrees of freedom in the vector of deviations from the hateful, ${\displaystyle \textstyle (x_{ane}-{\bar {ten}},\;\dots ,\;x_{n}-{\bar {x}}).}$

Taking square roots reintroduces bias (considering the square root is a nonlinear role, which does not commute with the expectation), yielding the corrected sample standard deviation, denoted by s:

${\displaystyle s={\sqrt {{\frac {1}{Northward-1}}\sum _{i=1}^{North}\left(x_{i}-{\bar {x}}\right)^{2}}}.}$

Equally explained in a higher place, while s ² is an unbiased estimator for the population variance, s is even so a biased estimator for the population standard deviation, though markedly less biased than the uncorrected sample standard deviation. This estimator is commonly used and generally known simply equally the "sample standard departure". The bias may however be large for small samples (North less than 10). As sample size increases, the corporeality of bias decreases. We obtain more information and the difference between ${\displaystyle {\frac {i}{North}}}$ and ${\displaystyle {\frac {one}{Northward-1}}}$ becomes smaller.

Unbiased sample standard divergence [edit]

For unbiased interpretation of standard divergence, in that location is no formula that works across all distributions, dissimilar for hateful and variance. Instead, south is used every bit a ground, and is scaled by a correction factor to produce an unbiased estimate. For the normal distribution, an unbiased figurer is given by s/c ₄, where the correction factor (which depends on N) is given in terms of the Gamma function, and equals:

${\displaystyle c_{4}(Northward)\,=\,{\sqrt {\frac {2}{Northward-1}}}\,\,\,{\frac {\Gamma \left({\frac {North}{ii}}\correct)}{\Gamma \left({\frac {Northward-i}{2}}\right)}}.}$

This arises because the sampling distribution of the sample standard departure follows a (scaled) chi distribution, and the correction factor is the mean of the chi distribution.

An approximation can exist given by replacing N − 1 with N − one.5, yielding:

${\displaystyle {\hat {\sigma }}={\sqrt {{\frac {1}{Due north-1.five}}\sum _{i=i}^{N}\left(x_{i}-{\bar {x}}\right)^{two}}},}$

The error in this approximation decays quadratically (as 1/N ⁱⁱ), and information technology is suited for all but the smallest samples or highest precision: for Due north = 3 the bias is equal to 1.iii%, and for N = 9 the bias is already less than 0.i%.

A more accurate approximation is to supercede ${\displaystyle North-i.5}$ above with ${\displaystyle N-one.5+1/(8(N-1))}$ .^[7]

For other distributions, the correct formula depends on the distribution, only a dominion of thumb is to apply the further refinement of the approximation:

${\displaystyle {\hat {\sigma }}={\sqrt {{\frac {1}{Due north-1.5-{\frac {i}{4}}\gamma _{ii}}}\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{ii}}},}$

where γ _ii denotes the population excess kurtosis. The excess kurtosis may be either known beforehand for certain distributions, or estimated from the data.^[viii]

Conviction interval of a sampled standard deviation [edit]

The standard difference we obtain past sampling a distribution is itself not absolutely authentic, both for mathematical reasons (explained here by the conviction interval) and for applied reasons of measurement (measurement error). The mathematical issue can be described by the confidence interval or CI.

To show how a larger sample volition make the confidence interval narrower, consider the post-obit examples: A minor population of North = 2 has simply one caste of freedom for estimating the standard divergence. The result is that a 95% CI of the SD runs from 0.45 × SD to 31.nine × SD; the factors hither are as follows:

${\displaystyle \Pr \left(q_{\frac {\blastoff }{ii}}<k{\frac {s^{ii}}{\sigma ^{2}}}<q_{ane-{\frac {\alpha }{two}}}\right)=i-\alpha ,}$

where ${\displaystyle q_{p}}$ is the p-thursday quantile of the chi-square distribution with k degrees of freedom, and ${\displaystyle 1-\alpha }$ is the conviction level. This is equivalent to the following:

${\displaystyle \Pr \left(thousand{\frac {south^{ii}}{q_{ane-{\frac {\alpha }{ii}}}}}<\sigma ^{2}<g{\frac {s^{two}}{q_{\frac {\alpha }{2}}}}\correct)=i-\alpha .}$

With k = ane, ${\displaystyle q_{0.025}=0.000982}$ and ${\displaystyle q_{0.975}=v.024}$ . The reciprocals of the foursquare roots of these two numbers give usa the factors 0.45 and 31.ix given higher up.

A larger population of N = x has 9 degrees of liberty for estimating the standard difference. The same computations every bit above give us in this instance a 95% CI running from 0.69 × SD to ane.83 × SD. So fifty-fifty with a sample population of 10, the actual SD tin still be almost a factor two higher than the sampled SD. For a sample population N=100, this is down to 0.88 × SD to 1.sixteen × SD. To exist more certain that the sampled SD is close to the actual SD we need to sample a large number of points.

These aforementioned formulae tin can exist used to obtain confidence intervals on the variance of residuals from a least squares fit under standard normal theory, where k is now the number of degrees of freedom for error.

Bounds on standard divergence [edit]

For a ready of N > four data spanning a range of values R, an upper bound on the standard difference s is given by south = 0.6R.^[9] An estimate of the standard difference for Northward > 100 information taken to be approximately normal follows from the heuristic that 95% of the area under the normal bend lies roughly two standard deviations to either side of the mean, so that, with 95% probability the total range of values R represents four standard deviations so that s ≈ R/4. This then-chosen range dominion is useful in sample size estimation, equally the range of possible values is easier to estimate than the standard divergence. Other divisors K(Northward) of the range such that s ≈ R/K(N) are bachelor for other values of N and for not-normal distributions.^[10]

Identities and mathematical properties [edit]

The standard deviation is invariant under changes in location, and scales directly with the scale of the random variable. Thus, for a abiding c and random variables Ten and Y:

${\displaystyle {\begin{aligned}\sigma (c)&=0\\\sigma (X+c)&=\sigma (X),\\\sigma (cX)&=|c|\sigma (X).\end{aligned}}}$

The standard deviation of the sum of two random variables can be related to their individual standard deviations and the covariance between them:

${\displaystyle \sigma (Ten+Y)={\sqrt {\operatorname {var} (X)+\operatorname {var} (Y)+two\,\operatorname {cov} (X,Y)}}.\,}$

where ${\displaystyle \textstyle \operatorname {var} \,=\,\sigma ^{2}}$ and ${\displaystyle \textstyle \operatorname {cov} }$ represent variance and covariance, respectively.

The calculation of the sum of squared deviations can be related to moments calculated directly from the data. In the following formula, the letter E is interpreted to hateful expected value, i.e., mean.

${\displaystyle \sigma (X)={\sqrt {\operatorname {E} \left[(Ten-\operatorname {E} [X])^{2}\correct]}}={\sqrt {\operatorname {E} \left[X^{2}\correct]-(\operatorname {E} [X])^{ii}}}.}$

The sample standard deviation can be computed as:

${\displaystyle s(X)={\sqrt {\frac {N}{N-1}}}{\sqrt {\operatorname {Due east} \left[(Ten-\operatorname {E} [10])^{2}\right]}}.}$

For a finite population with equal probabilities at all points, we have

${\displaystyle {\sqrt {{\frac {one}{N}}\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}={\sqrt {{\frac {1}{N}}\left(\sum _{i=1}^{N}x_{i}^{two}\right)-{\bar {10}}^{two}}}={\sqrt {\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\correct)-\left({\frac {1}{N}}\sum _{i=one}^{N}x_{i}\correct)^{two}}},}$

which means that the standard deviation is equal to the foursquare root of the divergence between the average of the squares of the values and the square of the boilerplate value.

See computational formula for the variance for proof, and for an coordinating issue for the sample standard deviation.

Estimation and application [edit]

Example of samples from two populations with the same mean merely different standard deviations. Red population has hateful 100 and SD 10; blue population has hateful 100 and SD fifty.

A big standard deviation indicates that the information points tin spread far from the mean and a small standard deviation indicates that they are clustered closely effectually the mean.

For instance, each of the three populations {0, 0, 14, 14}, {0, vi, 8, xiv} and {vi, 6, 8, 8} has a mean of 7. Their standard deviations are 7, 5, and 1, respectively. The third population has a much smaller standard divergence than the other 2 because its values are all close to 7. These standard deviations take the same units as the data points themselves. If, for case, the information set {0, half-dozen, 8, fourteen} represents the ages of a population of 4 siblings in years, the standard difference is v years. Every bit another example, the population {grand, 1006, 1008, 1014} may represent the distances traveled by iv athletes, measured in meters. It has a hateful of 1007 meters, and a standard deviation of 5 meters.

Standard difference may serve as a measure of doubtfulness. In physical science, for example, the reported standard deviation of a group of repeated measurements gives the precision of those measurements. When deciding whether measurements agree with a theoretical prediction, the standard deviation of those measurements is of crucial importance: if the mean of the measurements is too far away from the prediction (with the distance measured in standard deviations), so the theory beingness tested probably needs to be revised. This makes sense since they autumn outside the range of values that could reasonably be expected to occur, if the prediction were correct and the standard deviation appropriately quantified. Meet prediction interval.

While the standard divergence does measure how far typical values tend to be from the hateful, other measures are available. An example is the mean absolute deviation, which might exist considered a more than direct measure of boilerplate distance, compared to the root hateful square distance inherent in the standard divergence.

Application examples [edit]

The practical value of agreement the standard deviation of a set of values is in affectionate how much variation there is from the average (mean).

Experiment, industrial and hypothesis testing [edit]

Standard deviation is frequently used to compare existent-globe information against a model to test the model. For example, in industrial applications the weight of products coming off a production line may demand to comply with a legally required value. By weighing some fraction of the products an average weight can be constitute, which will always be slightly different from the long-term boilerplate. By using standard deviations, a minimum and maximum value can be calculated that the averaged weight will be within some very high percentage of the time (99.9% or more). If it falls outside the range then the product process may need to be corrected. Statistical tests such as these are particularly important when the testing is relatively expensive. For case, if the product needs to be opened and drained and weighed, or if the product was otherwise used up past the test.

In experimental scientific discipline, a theoretical model of reality is used. Particle physics conventionally uses a standard of "five sigma" for the declaration of a discovery. A v-sigma level translates to one chance in 3.5 million that a random fluctuation would yield the result. This level of certainty was required in order to assert that a particle consequent with the Higgs boson had been discovered in two independent experiments at CERN,^[xi] besides leading to the announcement of the first observation of gravitational waves,^[12] and confirmation of global warming.^[13]

Weather [edit]

As a simple example, consider the boilerplate daily maximum temperatures for ii cities, ane inland and one on the coast. It is helpful to understand that the range of daily maximum temperatures for cities nigh the coast is smaller than for cities inland. Thus, while these ii cities may each have the same average maximum temperature, the standard deviation of the daily maximum temperature for the littoral city volition be less than that of the inland metropolis as, on any particular day, the actual maximum temperature is more likely to be farther from the average maximum temperature for the inland city than for the coastal ane.

Finance [edit]

In finance, standard deviation is often used as a measure out of the hazard associated with cost-fluctuations of a given asset (stocks, bonds, property, etc.), or the risk of a portfolio of assets^[xiv] (actively managed mutual funds, index common funds, or ETFs). Risk is an important factor in determining how to efficiently manage a portfolio of investments because it determines the variation in returns on the asset and/or portfolio and gives investors a mathematical footing for investment decisions (known as mean-variance optimization). The key concept of adventure is that every bit information technology increases, the expected return on an investment should increase as well, an increase known as the risk premium. In other words, investors should expect a college return on an investment when that investment carries a higher level of run a risk or uncertainty. When evaluating investments, investors should judge both the expected return and the doubt of futurity returns. Standard deviation provides a quantified judge of the dubiety of futurity returns.

For example, assume an investor had to choose between 2 stocks. Stock A over the by 20 years had an average return of x per centum, with a standard deviation of 20 pct points (pp) and Stock B, over the same period, had average returns of 12 percent just a higher standard deviation of 30 pp. On the basis of risk and return, an investor may make up one's mind that Stock A is the safer choice, because Stock B's boosted two percentage points of return is not worth the additional 10 pp standard deviation (greater chance or dubiousness of the expected return). Stock B is likely to fall brusk of the initial investment (just besides to exceed the initial investment) more oft than Stock A under the same circumstances, and is estimated to return only two percentage more on boilerplate. In this example, Stock A is expected to earn nigh 10 percentage, plus or minus xx pp (a range of xxx per centum to −10 percent), most two-thirds of the time to come year returns. When considering more than farthermost possible returns or outcomes in time to come, an investor should expect results of every bit much equally x percent plus or minus 60 pp, or a range from 70 percentage to −l pct, which includes outcomes for iii standard deviations from the average render (nearly 99.7 percent of probable returns).

Calculating the average (or arithmetic mean) of the return of a security over a given menses will generate the expected return of the asset. For each catamenia, subtracting the expected return from the bodily return results in the difference from the mean. Squaring the difference in each period and taking the average gives the overall variance of the return of the asset. The larger the variance, the greater risk the security carries. Finding the foursquare root of this variance will give the standard deviation of the investment tool in question.

Population standard deviation is used to set up the width of Bollinger Bands, a technical analysis tool. For example, the upper Bollinger Band is given as ${\displaystyle \textstyle {\bar {x}}+northward\sigma _{x}.}$ The most normally used value for n is two; there is about a five percent gamble of going outside, assuming a normal distribution of returns.

Financial time series are known to be non-stationary series, whereas the statistical calculations to a higher place, such every bit standard deviation, apply only to stationary series. To apply the higher up statistical tools to non-stationary series, the series first must be transformed to a stationary series, enabling utilize of statistical tools that now take a valid basis from which to work.

Geometric interpretation [edit]

To gain some geometric insights and description, we will start with a population of three values, x _i, 10 _two, x _iii. This defines a bespeak P = (ten _ane, ten ₂, x ₃) in R ⁱⁱⁱ. Consider the line L = {(r, r, r) : r ∈ R}. This is the "chief diagonal" going through the origin. If our three given values were all equal, then the standard deviation would be zero and P would lie on L. So it is not unreasonable to assume that the standard divergence is related to the distance of P to Fifty. That is indeed the example. To move orthogonally from 50 to the bespeak P, one begins at the point:

${\displaystyle M=\left({\bar {ten}},{\bar {x}},{\bar {x}}\correct)}$

whose coordinates are the mean of the values we started out with.

Derivation of ${\displaystyle K=\left({\bar {x}},{\bar {ten}},{\bar {x}}\right)}$

${\displaystyle M}$ is on ${\displaystyle L}$ therefore ${\displaystyle Chiliad=(\ell ,\ell ,\ell )}$ for some ${\displaystyle \ell \in \mathbb {R} }$ . The line ${\displaystyle L}$ is to be orthogonal to the vector from ${\displaystyle Grand}$ to ${\displaystyle P}$ . Therefore: ${\displaystyle {\brainstorm{aligned}L\cdot (P-M)&=0\\[4pt](r,r,r)\cdot (x_{i}-\ell ,x_{2}-\ell ,x_{3}-\ell )&=0\\[4pt]r(x_{i}-\ell +x_{two}-\ell +x_{three}-\ell )&=0\\[4pt]r\left(\sum _{i}x_{i}-3\ell \right)&=0\\[4pt]\sum _{i}x_{i}-3\ell &=0\\[4pt]{\frac {ane}{iii}}\sum _{i}x_{i}&=\ell \\[4pt]{\bar {x}}&=\ell \end{aligned}}}$

A little algebra shows that the distance between P and Thousand (which is the same as the orthogonal distance between P and the line Fifty) ${\textstyle {\sqrt {\sum _{i}\left(x_{i}-{\bar {10}}\right)^{2}}}}$ is equal to the standard difference of the vector (x ₁, x _two, x ₃), multiplied by the square root of the number of dimensions of the vector (three in this case).

Chebyshev's inequality [edit]

An observation is rarely more than a few standard deviations away from the mean. Chebyshev's inequality ensures that, for all distributions for which the standard departure is defined, the amount of data within a number of standard deviations of the mean is at least as much as given in the following table.

Altitude from mean	Minimum population
${\displaystyle {\sqrt {2}}\,\sigma }$	fifty%
iiσ	75%
3σ	89%
4σ	94%
fiveσ	96%
6σ	97%
${\displaystyle k\sigma }$	${\displaystyle i-{\frac {i}{k^{2}}}}$ [fifteen]
${\displaystyle {\frac {1}{\sqrt {ane-\ell }}}\,\sigma }$	${\displaystyle \ell }$

Rules for commonly distributed data [edit]

Night blue is 1 standard deviation on either side of the mean. For the normal distribution, this accounts for 68.27 percent of the set up; while two standard deviations from the mean (medium and dark blue) business relationship for 95.45 pct; three standard deviations (calorie-free, medium, and dark blue) account for 99.73 pct; and four standard deviations account for 99.994 percent. The two points of the curve that are one standard deviation from the mean are besides the inflection points.

The fundamental limit theorem states that the distribution of an boilerplate of many contained, identically distributed random variables tends toward the famous bong-shaped normal distribution with a probability density function of

${\displaystyle f\left(10,\mu ,\sigma ^{2}\correct)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {ten-\mu }{\sigma }}\right)^{two}}}$

where μ is the expected value of the random variables, σ equals their distribution's standard deviation divided past n ^1/2, and n is the number of random variables. The standard deviation therefore is simply a scaling variable that adjusts how broad the curve will exist, though information technology also appears in the normalizing constant.

If a data distribution is approximately normal, then the proportion of data values within z standard deviations of the mean is divers by:

${\displaystyle {\text{Proportion}}=\operatorname {erf} \left({\frac {z}{\sqrt {two}}}\right)}$

where ${\displaystyle \textstyle \operatorname {erf} }$ is the error function. The proportion that is less than or equal to a number, 10, is given by the cumulative distribution office:

${\displaystyle {\text{Proportion}}\leq x={\frac {one}{2}}\left[1+\operatorname {erf} \left({\frac {10-\mu }{\sigma {\sqrt {2}}}}\right)\right]={\frac {ane}{2}}\left[i+\operatorname {erf} \left({\frac {z}{\sqrt {ii}}}\right)\right]}$ .^[16]

If a data distribution is approximately normal then about 68 percentage of the data values are inside 1 standard divergence of the mean (mathematically, μ ±σ, where μ is the arithmetic hateful), most 95 percent are within two standard deviations (μ ± iiσ), and well-nigh 99.7 per centum lie within iii standard deviations (μ ± 3σ). This is known as the 68–95–99.7 rule, or the empirical rule.

For various values of z, the percentage of values expected to lie in and outside the symmetric interval, CI = (−zσ,zσ), are as follows:

Confidence interval	Proportion within	Proportion without
	Percentage	Percentage	Fraction
0.318639 σ	25%	75%	3 / 4
0.674490 σ	50%	50%	1 / 2
0.977925 σ	66.6667%	33.3333%	1 / three
0.994458 σ	68%	32%	1 / 3.125
1σ	68.2689492 %	31.7310508 %	ane / 3.1514872
one.281552 σ	80%	20%	1 / v
1.644854 σ	90%	10%	1 / 10
ane.959964 σ	95%	5%	1 / 20
2σ	95.4499736 %	4.5500264 %	1 / 21.977895
2.575829 σ	99%	1%	1 / 100
3σ	99.7300204 %	0.2699796 %	1 / 370.398
three.290527 σ	99.9%	0.one%	1 / 1000
iii.890592 σ	99.99%	0.01%	i / 10000
4σ	99.993666 %	0.006334 %	1 / 15787
iv.417173 σ	99.999%	0.001%	i / 100000
4.5 σ	99.999320 465 3751%	0.000679 534 6249%	1 / 147159.5358 6.viii / 1000 000
4.891638 σ	99.9999%	0.0001%	1 / 1000 000
5σ	99.999942 6697 %	0.000057 3303 %	1 / one744 278
5.326724 σ	99.99999 %	0.00001 %	1 / 10000 000
v.730729 σ	99.999999 %	0.000001 %	one / 100000 000
six σ	99.999999 8027 %	0.000000 1973 %	one / 506797 346
half-dozen.109410 σ	99.9999999 %	0.0000001 %	1 / 1000 000 000
6.466951 σ	99.999999 99 %	0.000000 01 %	1 / x000 000 000
vi.806502 σ	99.999999 999 %	0.000000 001 %	ane / 100000 000 000
sevenσ	99.999999 999 7440%	0.000000 000 256 %	1 / 390682 215 445

Relationship between standard departure and mean [edit]

The mean and the standard deviation of a set of data are descriptive statistics normally reported together. In a certain sense, the standard divergence is a "natural" mensurate of statistical dispersion if the eye of the data is measured virtually the mean. This is because the standard divergence from the mean is smaller than from any other point. The precise argument is the following: suppose x _i, ..., x _n are real numbers and define the office:

${\displaystyle \sigma (r)={\sqrt {{\frac {i}{Due north-1}}\sum _{i=1}^{Due north}\left(x_{i}-r\right)^{ii}}}.}$

Using calculus or by completing the square, it is possible to show that σ(r) has a unique minimum at the mean:

${\displaystyle r={\bar {x}}.\,}$

Variability tin also be measured past the coefficient of variation, which is the ratio of the standard deviation to the mean. It is a dimensionless number.

Standard deviation of the mean [edit]

Often, we desire some data about the precision of the hateful we obtained. We can obtain this by determining the standard deviation of the sampled mean. Assuming statistical independence of the values in the sample, the standard departure of the hateful is related to the standard deviation of the distribution by:

${\displaystyle \sigma _{\text{mean}}={\frac {1}{\sqrt {N}}}\sigma }$

where N is the number of observations in the sample used to gauge the mean. This tin can easily exist proven with (see basic properties of the variance):

${\displaystyle {\brainstorm{aligned}\operatorname {var} (10)&\equiv \sigma _{X}^{2}\\\operatorname {var} (X_{1}+X_{2})&\equiv \operatorname {var} (X_{1})+\operatorname {var} (X_{ii})\\\end{aligned}}}$

(Statistical independence is assumed.)

${\displaystyle \operatorname {var} (cX_{i})\equiv c^{ii}\,\operatorname {var} (X_{1})}$

hence

${\displaystyle {\begin{aligned}\operatorname {var} ({\text{mean}})&=\operatorname {var} \left({\frac {ane}{N}}\sum _{i=1}^{N}X_{i}\right)={\frac {1}{Northward^{ii}}}\operatorname {var} \left(\sum _{i=1}^{N}X_{i}\right)\\&={\frac {1}{N^{2}}}\sum _{i=ane}^{N}\operatorname {var} (X_{i})={\frac {Due north}{N^{2}}}\operatorname {var} (Ten)={\frac {ane}{North}}\operatorname {var} (10).\finish{aligned}}}$

Resulting in:

${\displaystyle \sigma _{\text{mean}}={\frac {\sigma }{\sqrt {N}}}.}$

In gild to estimate the standard difference of the mean ${\displaystyle \sigma _{\text{hateful}}}$ it is necessary to know the standard divergence of the entire population ${\displaystyle \sigma }$ beforehand. Still, in most applications this parameter is unknown. For case, if a series of 10 measurements of a previously unknown quantity is performed in a laboratory, it is possible to calculate the resulting sample hateful and sample standard deviation, but it is impossible to summate the standard deviation of the hateful.

Rapid calculation methods [edit]

The following two formulas can stand for a running (repeatedly updated) standard deviation. A set of two power sums s _one and s ₂ are computed over a set up of Northward values of x, denoted every bit 10 ₁, ..., ten _N :

${\displaystyle s_{j}=\sum _{k=1}^{Due north}{x_{chiliad}^{j}}.}$

Given the results of these running summations, the values N, s _i, s _two can be used at whatever time to compute the current value of the running standard deviation:

${\displaystyle \sigma ={\frac {\sqrt {Ns_{2}-s_{1}^{2}}}{N}}}$

Where N, as mentioned in a higher place, is the size of the set of values (or can too be regarded as s ₀).

Similarly for sample standard departure,

${\displaystyle due south={\sqrt {\frac {Ns_{2}-s_{one}^{2}}{N(N-1)}}}.}$

In a estimator implementation, every bit the two due south _j sums become large, we need to consider round-off error, arithmetic overflow, and arithmetic underflow. The method beneath calculates the running sums method with reduced rounding errors.^[17] This is a "i pass" algorithm for calculating variance of n samples without the need to store prior data during the adding. Applying this method to a time series will event in successive values of standard difference corresponding to n data points as n grows larger with each new sample, rather than a abiding-width sliding window calculation.

For k = i, ..., n:

${\displaystyle {\begin{aligned}A_{0}&=0\\A_{g}&=A_{grand-1}+{\frac {x_{k}-A_{k-one}}{1000}}\end{aligned}}}$

where A is the hateful value.

${\displaystyle {\begin{aligned}Q_{0}&=0\\Q_{k}&=Q_{g-one}+{\frac {k-1}{k}}\left(x_{k}-A_{one thousand-1}\right)^{2}=Q_{k-1}+\left(x_{one thousand}-A_{g-1}\correct)\left(x_{k}-A_{k}\correct)\end{aligned}}}$

Annotation: ${\displaystyle Q_{1}=0}$ since ${\displaystyle k-1=0}$ or ${\displaystyle x_{one}=A_{ane}}$

Sample variance:

${\displaystyle s_{n}^{ii}={\frac {Q_{n}}{north-one}}}$

Population variance:

${\displaystyle \sigma _{n}^{2}={\frac {Q_{due north}}{north}}}$

Weighted calculation [edit]

When the values x_i are weighted with unequal weights west_i , the power sums s ₀, south _one, s ₂ are each computed as:

${\displaystyle s_{j}=\sum _{yard=1}^{N}w_{k}x_{thou}^{j}.\,}$

And the standard difference equations remain unchanged. s ₀ is now the sum of the weights and not the number of samples North.

The incremental method with reduced rounding errors can also be applied, with some additional complication.

A running sum of weights must be computed for each 1000 from 1 to north:

${\displaystyle {\brainstorm{aligned}W_{0}&=0\\W_{grand}&=W_{k-1}+w_{k}\end{aligned}}}$

and places where one/n is used above must exist replaced by w_i /W_{due north} :

${\displaystyle {\begin{aligned}A_{0}&=0\\A_{one thousand}&=A_{chiliad-1}+{\frac {w_{k}}{W_{k}}}\left(x_{k}-A_{one thousand-one}\right)\\Q_{0}&=0\\Q_{1000}&=Q_{thousand-1}+{\frac {w_{chiliad}W_{k-1}}{W_{1000}}}\left(x_{k}-A_{1000-1}\right)^{ii}=Q_{yard-1}+w_{k}\left(x_{one thousand}-A_{k-1}\right)\left(x_{k}-A_{chiliad}\correct)\end{aligned}}}$

In the terminal division,

${\displaystyle \sigma _{northward}^{two}={\frac {Q_{north}}{W_{n}}}\,}$

and

${\displaystyle s_{n}^{2}={\frac {Q_{northward}}{W_{n}-one}},}$

or

${\displaystyle s_{n}^{2}={\frac {n'}{n'-1}}\sigma _{n}^{2},}$

where northward is the total number of elements, and n' is the number of elements with non-zero weights.

The above formulas become equal to the simpler formulas given above if weights are taken equally equal to one.

History [edit]

The term standard deviation was commencement used in writing by Karl Pearson in 1894, following his employ of it in lectures.^{[18] [nineteen]} This was as a replacement for earlier alternative names for the aforementioned idea: for example, Gauss used mean error.^[20]

Higher dimensions [edit]

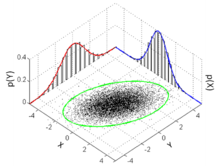
The standard deviation ellipse (green) of a two-dimensional normal distribution

In two dimensions, the standard departure tin can exist illustrated with the standard deviation ellipse (see Multivariate normal distribution § Geometric interpretation).

Run across also [edit]

• 68–95–99.7 dominion
• Accurateness and precision
• Chebyshev's inequality An inequality on location and scale parameters
• Coefficient of variation
• Cumulant
• Deviation (statistics)
• Altitude correlation Distance standard departure
• Mistake bar
• Geometric standard deviation
• Mahalanobis distance generalizing number of standard deviations to the mean
• Hateful absolute error
• Pooled variance
• Propagation of dubiety
• Percentile
• Raw data
• Robust standard departure
• Root mean foursquare
• Sample size
• Samuelson's inequality
• Six Sigma
• Standard error
• Standard score
• Yamartino method for calculating standard departure of current of air direction

References [edit]

1. ^ Bland, J.K.; Altman, D.G. (1996). "Statistics notes: measurement fault". BMJ. 312 (7047): 1654. doi:10.1136/bmj.312.7047.1654. PMC2351401. PMID 8664723.
2. ^ Gauss, Carl Friedrich (1816). "Bestimmung der Genauigkeit der Beobachtungen". Zeitschrift für Astronomie und Verwandte Wissenschaften. 1: 187–197.
3. ^ Walker, Helen (1931). Studies in the History of the Statistical Method. Baltimore, Doc: Williams & Wilkins Co. pp. 24–25.
4. ^ Weisstein, Eric W. "Bessel'south Correction". MathWorld.
5. ^ "Standard Deviation Formulas". www.mathsisfun.com . Retrieved 21 August 2020.
6. ^ Weisstein, Eric West. "Standard Divergence". mathworld.wolfram.com . Retrieved 21 August 2020.
7. ^ Gurland, John; Tripathi, Ram C. (1971), "A Elementary Approximation for Unbiased Estimation of the Standard Difference", The American Statistician, 25 (four): 30–32, doi:10.2307/2682923, JSTOR 2682923
8. ^ "Standard Deviation Calculator". PureCalculators. 11 July 2021. Retrieved xiv September 2021.
9. ^ Shiffler, Ronald E.; Harsha, Phillip D. (1980). "Upper and Lower Premises for the Sample Standard Deviation". Teaching Statistics. 2 (3): 84–86. doi:x.1111/j.1467-9639.1980.tb00398.x.
10. ^ Browne, Richard H. (2001). "Using the Sample Range as a Basis for Calculating Sample Size in Ability Calculations". The American Statistician. 55 (four): 293–298. doi:10.1198/000313001753272420. JSTOR 2685690. S2CID 122328846.
11. ^ "CERN experiments observe particle consistent with long-sought Higgs boson | CERN press part". Printing.web.cern.ch. 4 July 2012. Archived from the original on 25 March 2016. Retrieved 30 May 2015.
12. ^ LIGO Scientific Collaboration, Virgo Collaboration (2016), "Ascertainment of Gravitational Waves from a Binary Black Pigsty Merger", Physical Review Messages, 116 (vi): 061102, arXiv:1602.03837, Bibcode:2016PhRvL.116f1102A, doi:10.1103/PhysRevLett.116.061102, PMID 26918975, S2CID 124959784
13. ^ Alister Doyle (25 February 2019). "Prove for man-made global warming hits 'gold standard': scientists". Reuters . Retrieved 23 March 2021.
14. ^ "What is Standard Deviation". Pristine. Retrieved 29 Oct 2011.
15. ^ Ghahramani, Saeed (2000). Fundamentals of Probability (2nd ed.). New Jersey: Prentice Hall. p. 438.
16. ^ Eric W. Weisstein. "Distribution Function". MathWorld—A Wolfram Spider web Resource. Retrieved 30 September 2014.
17. ^ Welford, BP (August 1962). "Note on a Method for Calculating Corrected Sums of Squares and Products". Technometrics. 4 (3): 419–420. CiteSeerX10.1.1.302.7503. doi:10.1080/00401706.1962.10490022.
18. ^ Dodge, Yadolah (2003). The Oxford Dictionary of Statistical Terms . Oxford University Printing. ISBN978-0-nineteen-920613-1.
19. ^ Pearson, Karl (1894). "On the dissection of asymmetrical frequency curves". Philosophical Transactions of the Royal Society A. 185: 71–110. Bibcode:1894RSPTA.185...71P. doi:10.1098/rsta.1894.0003.
20. ^ Miller, Jeff. "Primeval Known Uses of Some of the Words of Mathematics".

External links [edit]

• "Quadratic deviation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Standard Departure Figurer"

kingdism1943.blogspot.com

Source: https://en.wikipedia.org/wiki/Standard_deviation

Share this post